Сезонные базовые линии

Применение Ключ-АСТРОМ / ИИ/ Сезонные базовые линии

Сезонный базовый уровень представляет собой динамический подход к базовому уровню, при котором системы имеют различные сезонные модели. Примером сезонного шаблона является показатель, который повышается в рабочее время и остается низким вне его. В таком случае сложно настроить конфигурацию оповещения на основе статического или автоадаптивного порога. Если вы установите фиксированный порог, основанный на поведении рабочего времени, вы пропустите аномалию в нерабочее время. Искусственный интеллект изучает сезонное поведение ваших показателей и автоматически создает для него доверительный диапазон.

Когда конфигурация события метрики включает несколько объектов, каждый объект получает свой собственный сезонный базовый уровень, и каждый базовый уровень оценивается независимо. Например, если масштаб события включает пять сервисов, Ключ-АСТРОМ рассчитывает и оценивает пять независимых базовых уровней.

Пример базового уровня

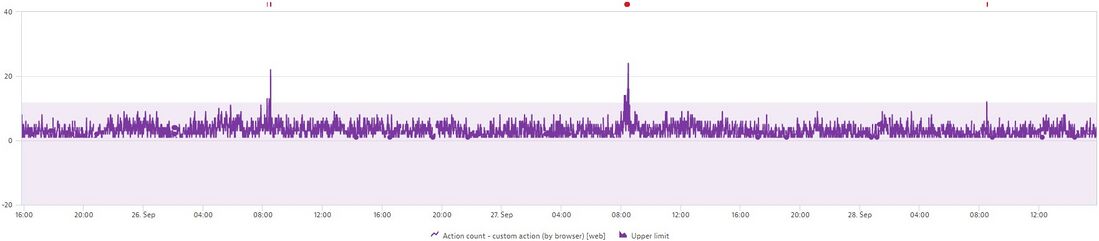
Рассмотрим пример, в котором сезонный базовый уровень имеет преимущество перед несезонным порогом. На приведенной ниже диаграмме показано измерение действий пользователя в приложении. Как вы можете видеть, дневные пики наблюдаются примерно в 8 утра. При оценке с помощью автоадаптивного порога эти пики приводят к ложноположительным результатам (красные метки над графиком).

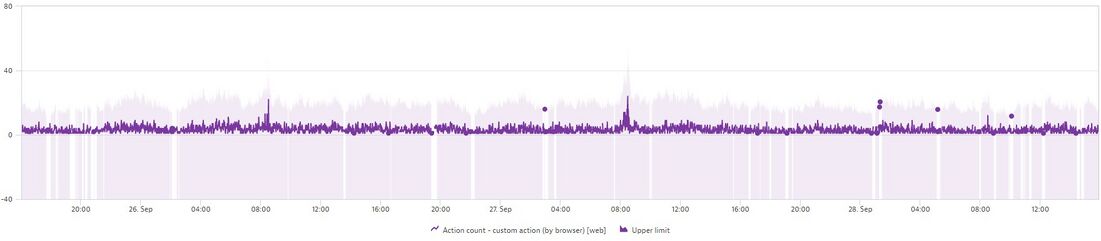
ИИ автоматически проверяет, соответствуют ли условия сезонной модели, и создает доверительный диапазон на основе сезонной модели. Как вы можете видеть на приведенной ниже диаграмме, модель распознает сезонность и не генерирует ложных срабатываний на пиках. Тем не менее, он все равно вызовет предупреждение, если всплеск произойдет в другое время.

Параметры базовой модели

Модель сезонного базового уровня использует значения показателей за каждую минуту в течение последних 14 дней в качестве эталона для расчета базового уровня. Модель изучает обычное поведение показателя и нацелена на обнаружение регулярно повторяющихся закономерностей. Она использует вероятностный прогноз для вычисления доверительной полосы, которая охватывает ожидаемый диапазон будущей точки.

Вы можете настроить ширину доверительной полосы с помощью параметра tolerance. Более высокий допуск означает более широкую доверительную полосу, что приводит к меньшему количеству запускаемых событий. Допустимый диапазон допуска составляет от 0.1 до 10, 4 в качестве значения по умолчанию.

Как следует из названия, сезонная модель полезна для данных с сезонными закономерностями (например, дневными пиками). Поскольку он потребляет значительные ресурсы и требует больше времени для изучения поведения, существуют некоторые проверки для обеспечения оптимальной производительности. При проверке оценивается каждый кортеж (уникальные комбинации метрика—измерение—значение измерения). Если пропуска нет, вместо него используется простая модель с соответствующим сообщением, отображаемым в предварительном просмотре.

Простая модель вычисляет доверительный диапазон на основе надежной оценки распределения входных данных, и ее расчетный интервал остается постоянным с течением времени. Для простой модели параметр tolerance управляет шириной доверительной полосы таким же образом, как и для сезонной модели.

Если в метаданных метрики заданы границы метрики (минимальное или максимальное значение метрики), они автоматически учитываются в модели. Если границы метрики не заданы и входные данные содержат только положительные значения, модель автоматически устанавливает минимальное граничное значение 0. Если найдено минимальное или максимальное значение, доверительный диапазон не превышает этого значения.

Модель (будь то сезонная или простая) обновляется ежедневно.

Другим важным параметром для сезонных базовых уровней является скользящее окно, которое используется для сравнения текущих измерений с доверительным диапазоном. Он определяет, как часто должен нарушаться доверительный интервал в течение скользящего периода времени, чтобы вызвать событие (нарушения не обязательно должны быть последовательными). Такой подход помогает уменьшить количество ложных срабатываний при оповещении. Вы можете установить скользящее окно максимум на 60 минут.

Обучение базовой модели

Сезонная базовая модель использует значения показателей за каждую минуту в течение последних 14 дней для обучения и обучается по кортежу (уникальные комбинации метрика—измерение—значение измерения). Обучение происходит ежедневно.

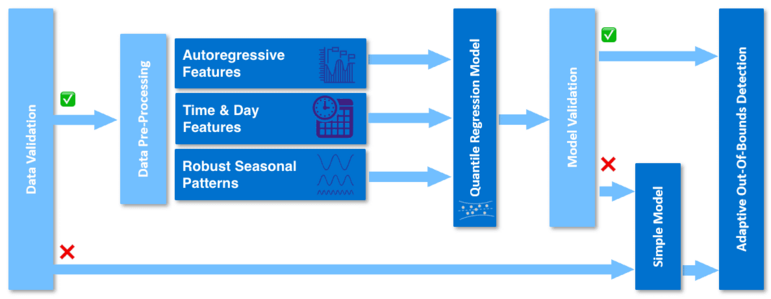
На изображении ниже представлен обзор тренировочного процесса.

Первый шаг, проверка данных, гарантирует целесообразность обучения сезонной модели на данных показателей. Вот несколько причин для перехода к простой модели:

• в данных отсутствует много значений
• данные имеют много отклонений
• данные недостаточно изменчивы
• в данных не обнаруживается сезонности.

Если эта проверка завершается неудачей, вместо нее используется простая модель. Если проверка прошла успешно, следующим шагом является предварительная обработка входных данных. На этом этапе данные подготавливаются для обучения модели квантильной регрессии, которая изучает сезонное поведение на основе трех основных характеристик данных:

• Объекты авторегрессии представляют собой исторические точки данных (небольшие пробелы интерполированы).
• Функции времени и суток определяют день или конкретное время суток, которые могут помочь изучить закономерность, происходящую только в определенный день
• Надежные сезонные паттерны описывают регулярно повторяющиеся паттерны, извлеченные с помощью преобразования Фурье.

Эти функции используются для обучения модели квантильной регрессии, вероятностной регрессионной модели, которая устойчива к выбросам из-за оценки квантилей.

Следующим шагом является валидация модели, которая проверяет надежность прогнозируемых квантилей на подмножестве данных. Если эта проверка завершается неудачей, вместо нее используется простая модель.

После завершения обучения Ключ-АСТРОМ использует сезонную модель для обнаружения аномалий. Каждую минуту модель выдает прогноз на один шаг вперед доверительного диапазона на следующую минуту. Как только поступает фактическая точка данных, прогнозируемый доверительный интервал сравнивается с фактическим значением, чтобы проверить, находится ли значение в прогнозируемых границах.